How To Find Coefficient of Variation in Microsoft Excel
Microsoft Excel enables users to calculate the coefficient of variation (CV), a statistical measure of relative variability within a data set. By understanding how to compute the CV, you’ll gain insights into the consistency of your data, allowing for a deeper analysis and more reliable conclusions.

How To Find Coefficient of Variation in Microsoft Excel
Understanding the dispersion of your data is crucial for in-depth analysis and the coefficient of variation provides this insight by comparing the standard deviation to the mean. Here’s how you can calculate it in Microsoft Excel.
-
Step 1. Organize Your Data
Open your Excel workbook and ensure your data is organized in one column for easy analysis. This column should represent the data set for which you wish to calculate the coefficient of variation.
-
Step 2. Calculate the Mean
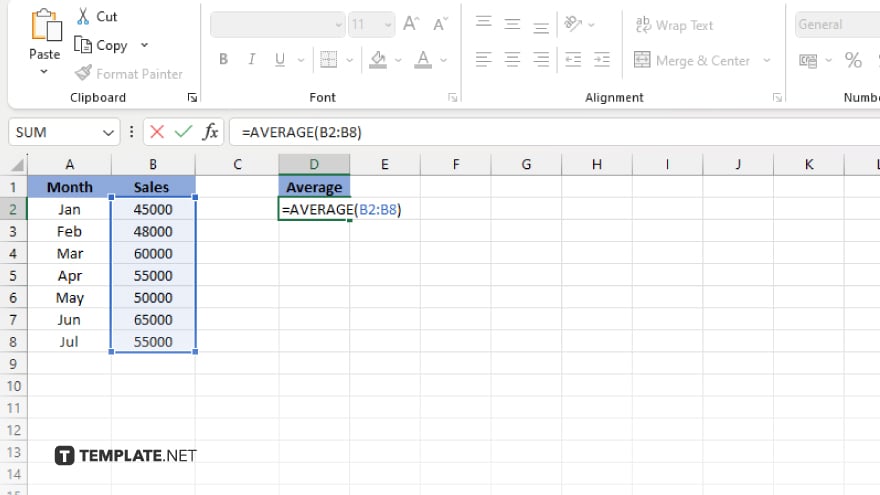
Above or below your data set, find an empty cell to calculate the mean (average). Use the formula “=AVERAGE(range),” where “range” is the cell range of your data set. For example, if your data is in cells A2 through A21, your formula would be “=AVERAGE(A2:A21).”
-
Step 3. Calculate the Standard Deviation
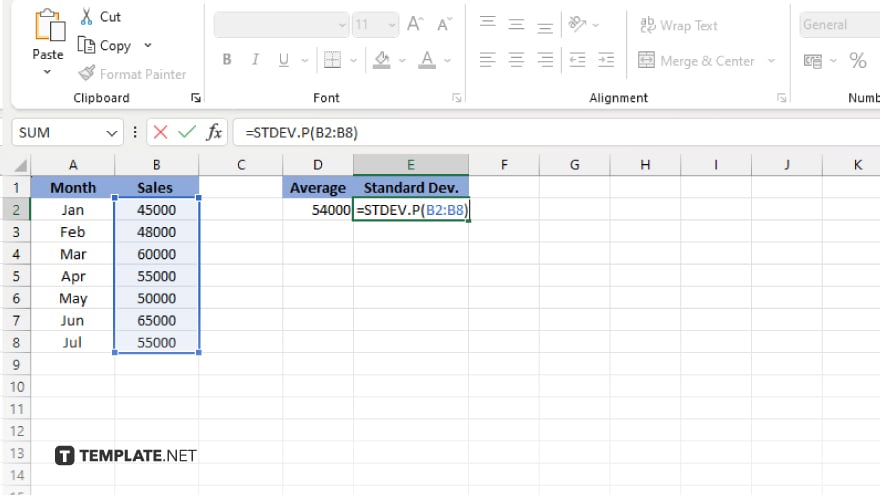
In a new cell of your sheet, calculate the standard deviation of your data set using the formula “=STDEV.P(range)” for a population standard deviation or “=STDEV.S(range)” for a sample standard deviation. Replace “range” with your actual data range.
-
Step 4. Calculate the Coefficient of Variation
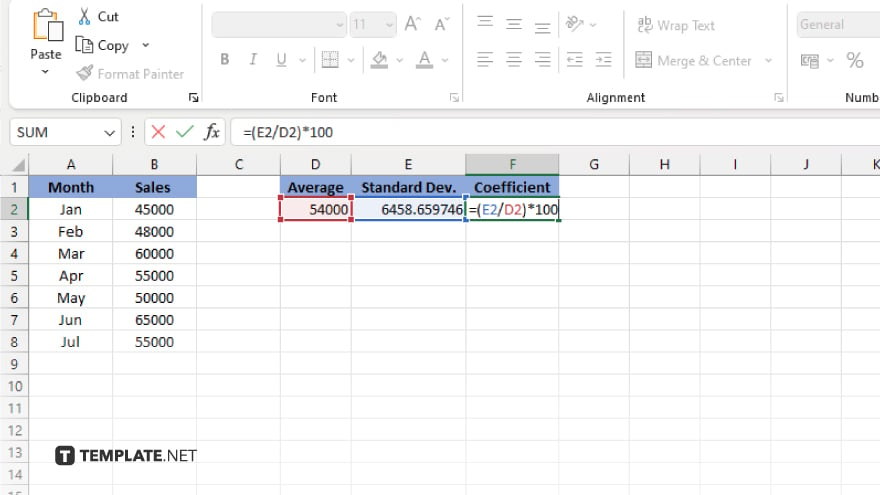
In another empty cell of your worksheet, calculate the coefficient of variation by dividing the standard deviation by the mean and then multiplying by 100 to express it as a percentage. Use the formula “=(STDEV.P(range)/AVERAGE(range))*100” for population data or “=(STDEV.S(range)/AVERAGE(range))*100” for sample data.
-
Step 5. Interpret the Results
The resulting value represents your data’s coefficient of variation, indicating the extent of variability in relation to the mean. A higher CV suggests more dispersion, while a lower CV indicates less variability relative to the mean.
You may also find valuable insights in the following articles offering tips for Microsoft Excel:
FAQs
What formula do I use to calculate the coefficient of variation in Excel?
Use “=(STDEV.P(range)/AVERAGE(range))*100” for the entire population or “=(STDEV.S(range)/AVERAGE(range))*100” for a sample.
Can the coefficient of variation be calculated if some of my data points are zeros?
Yes, but the presence of zeros can significantly affect the CV, especially if the mean of the dataset is small.
Is the coefficient of variation a better measure than standard deviation?
The coefficient of variation is useful for comparing variability between datasets with different units or means, while standard deviation is used for datasets within the same scale.
How do I interpret the coefficient of variation in Excel?
A higher coefficient of variation indicates greater data variability relative to the mean, and a lower coefficient suggests less variability.
Can I calculate the coefficient of variation for multiple datasets in Excel at once?
Yes, you can calculate it for multiple datasets by applying the same formula to different ranges within your Excel sheet, ensuring each range is correctly specified in each formula.






